V článku Least-to-Most Prompting Enables Complex Reasoning in Large Language Models], který navrhli Zhou a kol. z Google Research, je metoda Least-to-most prompting novou metodou, jejímž cílem je zlepšit schopnost řešení problémů ve velkých jazykových modelech.
Metoda vychází z pedagogické psychologie a spočívá v rozkladu složitých problémů na jednodušší, postupné podproblémy, přičemž využívá odpovědi z předchozích podproblémů k usnadnění řešení následujících.
Implementace metody „least-to-most prompting“ nevyžaduje trénování modelu ani jeho dolaďování.
Provádí se výhradně prostřednictvím několika podnětů, což se účinně projevilo v úlohách, jako je symbolická manipulace, kompoziční zobecnění (schopnost naučit se význam slov a následně je asociací aplikovat na jiné pojmy) a matematické uvažování.
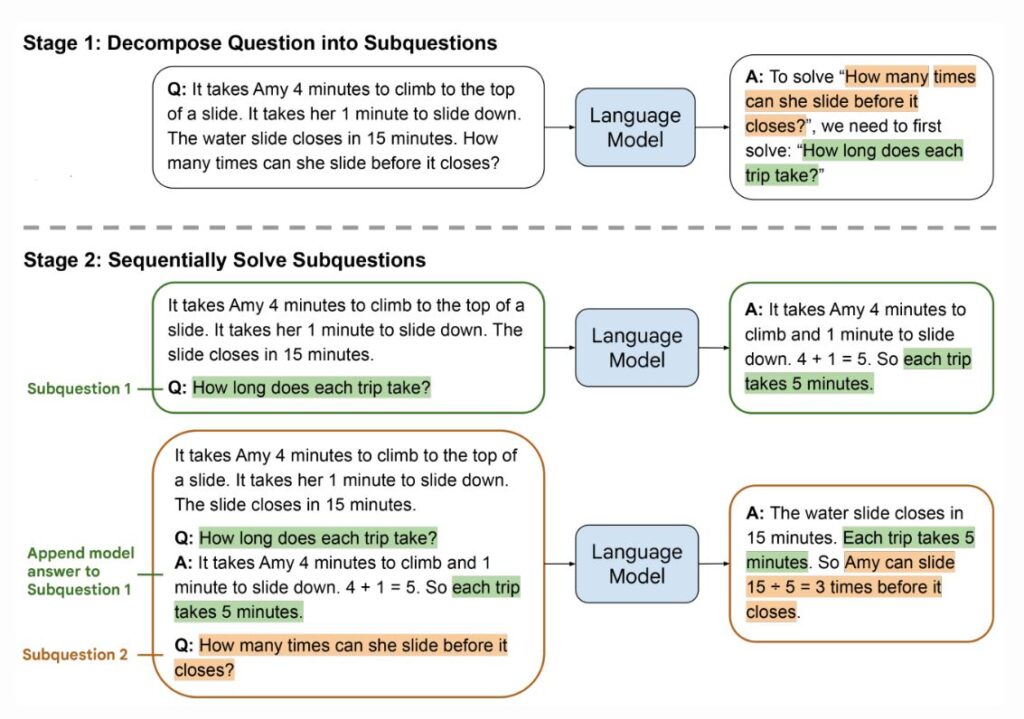
Následující obrázek z článku ukazuje řešení matematické slovní úlohy metodou least-to-most ve dvou fázích: (1) dotaz na jazykový model pro rozklad úlohy na dílčí úlohy; (2) dotaz na jazykový model pro postupné řešení dílčích úloh. Odpověď na druhý podproblém je postavena na odpovědi na první podproblém.
Demonstrační příklady pro výzvu každé fáze jsou v této ilustraci vynechány.
Podstata této metody spočívá v rozdělení složitého problému do dvou fází:
Fáze rozčlenění problému: Model je vyzván, aby problém zredukoval na více dílčích problémů.
Fáze sekvenčního řešení: Model postupně řeší tyto dílčí problémy, přičemž odpověď na každý následující dílčí problém vychází z odpovědí na problémy předchozí.
Fáze 1: Jazykový model (LM) je požádán o zredukování složitého problému na jednodušší podproblémy. V tomto případě, LM rozloží původní otázku „Kolikrát může Amy sklouznout po skluzavce před tím, než se uzavře?“ na podproblém „Jak dlouho trvá každý výstup a skluz?“
Fáze 2: LM postupně řeší podproblémy. Nejprve odpoví na první podproblém, zjistí, že každý výstup a skluz trvá dohromady 5 minut (4 minuty nahoru, 1 minuta dolů). Poté použije tuto informaci k řešení druhého podproblému, který zní „Kolikrát může Amy sklouznout před tím, než se skluzavka uzavře?“. Vypočítá to tak, že vezme dobu, po kterou skluzavka zůstává otevřená (15 minut), a vydělí ji dobou jednoho výstupu a skluzu (5 minut), čímž získá odpověď, že Amy může sklouznout třikrát.
Představ si, že máme velký dort a chceme zjistit, kolik kousků můžeme z něj vykrojit, než bude celý snědený. Dort je ale tak velký, že není jednoduché hned říct, kolik kousků z něj dostaneme. Co s tím?
Použijeme metodu krok za krokem:
Rozdělení dortu: Nejdříve si představíme, že máme menší dortíky a každý z nich můžeme rozdělit na 5 kousků. To je jednodušší než počítat kousky z jednoho obrovského dortu.
Počítání kousků: Pak spočítáme, kolikrát můžeme vykrojit 5 kousků z menších dortíků, než budou všechny snědené. Když víme, že máme čas sníst jenom 3 menší dortíky, víme, že získáme 3 × 5 = 15 kousků.
Představ si, že máš pytlík a v něm jsou kuličky. Chceš je všechny vysypat, ale můžeš vyndat jen jednu kuličku za minutu a navíc, máš na to jenom 15 minut, pak musíš jít spát.
Nyní, abychom to vyřešili, rozdělíme si úkol:
Zjistíme, jak dlouho trvá vyndat kuličku: Nejdříve zjistíme, jak dlouho trvá vyndat jednu kuličku z pytlíku, což je právě ta 1 minuta.
Spočítáme, kolik kuliček můžeme vyndat: Teď víme, že na vyndání jedné kuličky máme 1 minutu a celkem máme 15 minut. Takže se děti snadno dostanou k tomu, že za 15 minut vyndají 15 kuliček, protože 15 (minut) děleno 1 (minuta na kuličku) je 15 kuliček.